Posts

Please see original post for full version. Neural Tangent Kernel (NTK) is well known as a powerful tool that elegantly proves the convergence and generalisation of neural networks. However, as an engineering student who basically know nothing about mathematics, I find the original NTK paper a little bit opaque to understand. Driven by my intrinsic inquisitiveness (“vegetable but addicted”), I spent some time trying to figure out what on earth is NTK with every effort and managed to get an impression on that at last. This article aims to help people who are in the same boat, vegetable, but still struggling for a free ride in deep learning theory.

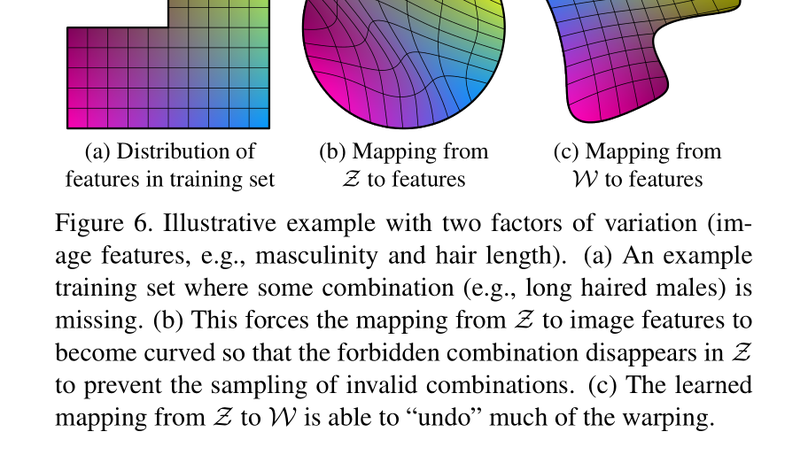
Please see original post for full version. Path length regularisation is a new trick for training GAN (i.e. Generative Adversarial Networks) proposed by NVIDIA in their StyleGAN2 paper. In appendix C of the paper, authors of which provide its readers with somewhat obscure explanations of the effects of the trick, leaving novices like me greatly baffled. In this article, I will decompose the whole theory into more detailed proofs of several lemmas respectively, targeting at a deeper comprehension of this prominent piece of art.

Please see original post for full version. When I was reading this famous paper I found it quite opaque for people as vegetable as I am. Things like “Sobolev norm”, “Kantorovich-Rubinstein duality”, “Pinsker’s inequality” and “Sard’s Lemma” make me feel like an alien who has never learned mathematics on this planet. Besides, some of the proofs are succinct or “is trivial and left as an exercise to the reader”. This article may not aim to explain those intoxicating mathematical terminologies, but to provide more detailed proofs within my ability.

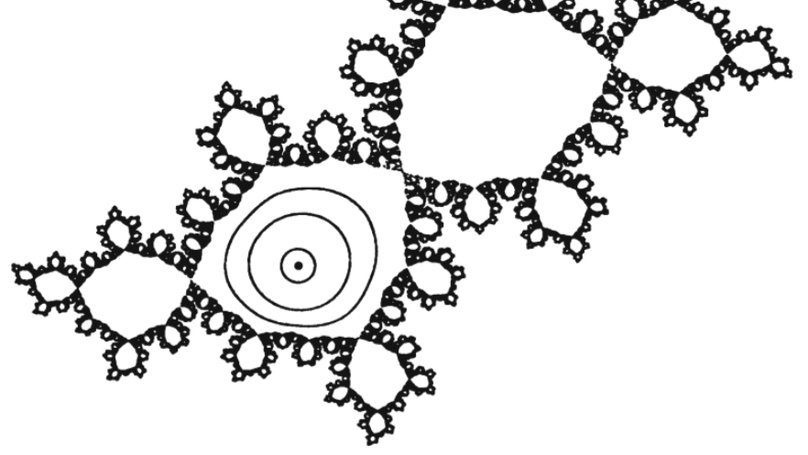
Please see original post for full version. Recently I’ve been studying complex dynamics by myself. As its name suggests this is such a complicated branch of mathematics that requires solid foundation in complex analysis, measure theory, set theory and so on for people to understand what it is talking about. Maybe I exaggerate. Whatever, in this article I’ll show some exploration results of a kind of topological construction of Fatou stable area, Siegel disc, named after its finder, with the help of Matplotlib (a famous side-package of Python specializes in visualization).

Please see original post for full version. 4 integers between 1 to 20, as well as 7 kinds of operations (including addition, subtraction, multiplication, division, logarithm, factorial and exponentiation), are the only things allowed in approximating the irrational number, Pi. Each integer can merely appear once in the final equation you submit eventually, but appearing times of those calculating signs is unlimited.